[알고리즘] Time Complexity / greedy Algorithm / implementation

알고리즘은 문제를 해결하는 최선의 선택입니다.

1. 문제를 이해하고

2. 전략을 세우고 (수도코드, 흐름의 그림, 페어에게 설명)

3. 이에 따라 코드 작성으로 문제 해결

개발자로서 만나게 될 대부분의 개발 태스크는 알고리즘 문제만큼 어렵지 않습니다. 그러나 새로운 문제에 봉착했을 때, 전략과 알고리즘을 구상하여 실제로 코드로 구현해 보는 경험은 매우 중요합니다. 많은 기업에서 주니어 개발자를 채용할 때에, 알고리즘 풀이를 통해 지원자의 역량을 가늠합니다. 알고리즘 풀이를 통해 지원자의 로직과 문제해결 방식을 확인하고, 이를 통해 개발자다운 사고방식을 보게 된다고 합니다.

1. Time Complexity

알고리즘 문제를 풀때 해결하는것도 가장 중요하지만 효율적인 알고리즘을 찾는 것 또한 중요합니다.

효율적인 방법을 찾는다는 것은 시간복잡도를 고민하는 것과 같은 의미 입니다.

시간복잡도는 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가? 를 뜻합니다.

제 생각을 적어보자면 해결만 하면 되었지 왜 시간복잡도를 고려해 가면서 문제 해결을 해야하나 라는 의문이 가지기 쉬울겁니다. 저 또한 그러한 생각을 가지고 있었습니다. 하지만 고객이 100명밖에 없는 서비스와, 100만명이 이용하는 서비스는 컴퓨터가 처리해야할 자료의 양의 차이가 날 겁니다. 보통 스타트업의 이야기를 들어보면 1000명의 고객을 유지하다가 10배, 100배로 늘어나게 되었을 때에 코드를 보수하는게 아닌 뜯어고쳐서 새로 만든다는 이야기를 많이 들었습니다. 그렇기 때문에 알고리즘, 시간복잡도를 생각하는 것 같습니다.

시간 복잡도를 표현 할 때에 사용하는 표기법은 Big-0 표기 법을 사용합니다.

Big-O(빅-오)
Big-Ω(빅-오메가)
Big-θ(빅-세타)

시간 복잡도를 각각 최악, 최선, 중간(평균)의 경우에 대하여 나타내는 방법입니다.

빅오 표기법은 최악의 경우를 고려하므로, 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있기 때문입니다.

"최소한 특정 시간 이상이 걸린다" 혹은 "이 정도 시간이 걸린다"를 고려하는 것보다 "이 정도 시간까지 걸릴 수 있다"를 고려해야 그에 맞는 대응이 가능합니다.

1) O(1)

입력값이 증가하더라도 시간이 늘어나지 않습니다. 다시 말해 입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다는 의미입니다.

function O_1_algorithm(arr, index) {
	return arr[index];
}

let arr = [1, 2, 3, 4, 5];
let index = 1;
let result = O_1_algorithm(arr, index);
console.log(result); // 2

입력값의 크기가 아무리 커져도 즉시 출력값을 얻어낼 수 있습니다. 예를 들어 arr의 길이가 100만이라도, 즉시 해당 index에 접근해 값을 반환할 수 있습니다.

2) O(n)

linear complexity라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미합니다.

예를 들어 입력값이 1일 때 1초의 시간이 걸리고, 입력값을 100배로 증가시켰을 때 1초의 100배인 100초가 걸리는 알고리즘을 말합니다.

function O_n_algorithm(n) {
	for (let i = 0; i < n; i++) {
	// do something for 1 second
	}
}

function another_O_n_algorithm(n) {
	for (let i = 0; i < 2n; i++) {
	// do something for 1 second
	}
}

O_n_algorithm 함수

입력값(n)이 1 증가할 때마다 코드의 실행 시간이 1초씩 증가합니다.

another_O_n_algorithm 함수

입력값이 1 증가할때마다 코드의 실행 시간이 2초씩 증가합니다. 이것을 보고, "아! 그렇다면 이 알고리즘은 O(2n) 이라고 표현하겠구나!" 라고 생각할 수 있습니다. 그러나, 사실 이 알고리즘 또한 Big-O 표기법으로는 O(n)으로 표기합니다. 입력값이 커지면 커질수록 계수(n 앞에 있는 수)의 의미(영향력)가 점점 퇴색되기 때문에, 같은 비율로 증가하고 있다면 2배가 아닌 5배, 10배로 증가하더라도 O(n)으로 표기합니다.

3) O(log n)

logarithmic complexity라고 부르며 Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도를 가집니다.

자료구조에서 배웠던 BST(Binary Search Tree)에선 원하는 값을 탐색할 때, 노드를 이동할 때마다 경우의 수가 절반으로 줄어듭니다.

이해하기 쉬운 게임으로 비유해 보자면 up & down을 예로 들 수 있습니다.

1~100 중 하나의 숫자를 플레이어1이 고른다 (30을 골랐다고 가정합니다).
50(가운데) 숫자를 제시하면 50보다 작으므로 down을 외친다.
1~50중의 하나의 숫자이므로 또다시 경우의 수를 절반으로 줄이기 위해 25를 제시한다.
25보다 크므로 up을 외친다.
경우의 수를 계속 절반으로 줄여나가며 정답을 찾는다.

매번 숫자를 제시할 때마다 경우의 수가 절반이 줄어들기 때문에 최악의 경우에도 7번이면 원하는 숫자를 찾아낼 수 있게 됩니다. BST의 값 탐색도 같은 로직으로 O(log n)의 시간 복잡도를 가진 알고리즘(탐색기법)입니다.

4) O(n^2)

quadratic complexity라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미합니다.

1일 경우 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 된다면, 이 알고리즘의 시간 복잡도는 O(n2)라고 표현합니다.

function O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
		// do something for 1 second
		}
	}
}

function another_O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
			for (let k = 0; k < n; k++) {
			// do something for 1 second
			}
		}
	}
}

2n, 5n 을 모두 O(n)이라고 표현하는 것처럼, n3과 n5 도 모두 O(n2)로 표기합니다. n이 커지면 커질수록 지수가 주는 영향력이 점점 퇴색되기 때문에 이렇게 표기합니다.

반복문이라는게 참 편리하다고 느꼈는데 시간복잡도에서 오래걸리는 코드중 하나입니다. 편하다고 느꼈던게 무지성으로 반복하기 때문에 편리하다고 느꼈다고 생각합니다.

5)O(2^n)

exponential complexity라고 부르며 Big-O 표기법 중 가장 느린 시간 복잡도를 가집니다.

종이를 42번 접으면 그 두께가 지구에서 달까지의 거리보다 커진다는 이야기를 과학시간 또는 수학시간에 들어보았을 겁니다. 저에겐 충격이어서 시도도 해보았을 정도였습니다. (그렇기 때문에 못들어 봤으면 수업시간에 잔거..) 고작 42번 만에 얇은 종이가 그만한 두께를 가질 수 있는 것은, 매번 접힐 때마다 두께가 2배로 늘어나기 때문입니다. 구현한 알고리즘의 시간 복잡도가 O(2n)이라면 다른 접근 방식을 고민해 보는 것이 좋습니다.

function fibonacci(n) {
	if (n <= 1) {
		return 1;
	}
	return fibonacci(n - 1) + fibonacci(n - 2);
}

재귀로 구현하는 피보나치 수열은 O(2^n)의 시간 복잡도를 가진 대표적인 알고리즘입니다. 브라우저 개발자 창에서 n을 40으로 두어도 수초가 걸리는 것을 확인할 수 있으며, n이 100 이상이면 평생 결과를 반환받지 못할 수도 있습니다. 그래서 잘못하면 브라우저가 꺼질수도 있습니다.

Advanced

일반적으로 코딩 테스트에서는 정확한 값을 제한된 시간 내에 반환하는 프로그램을 작성해야 합니다. 컴파일러 혹은 컴퓨터의 사양에 따라 차이는 있겠지만, 시간제한과 주어진 데이터 크기 제한에 따른 시간 복잡도를 어림잡아 예측해 보는 것은 중요합니다.

예를 들어 입력으로 주어지는 데이터에는 n만큼의 크기를 가지는 데이터가 있고, n이 1,000,000보다 작은 수일 때 O(n) 혹은 O(nlogn)의 시간 복잡도를 가지도록 예측하여 프로그램을 작성할 수 있습니다.

n^2의 시간 복잡도를 예측할 수 없는 이유는 실제 수를 대입해 계산해보면 유추할 수 있습니다. 1,000,0002은 즉시 처리하기에 무리가 있는 숫자입니다. (1,000,000 * 1,000,000 = 1,000,000,000,000) 만약 n ≤ 500 으로 입력이 제한된 경우에는 O(n^3)의 시간 복잡도를 가질 수 있다고 예측할 수 있습니다. O(n^3)의 시간 복잡도를 가지는 프로그램을 작성한다면 문제를 금방 풀 수 있을 텐데, 시간 복잡도를 O(log n)까지 줄이기 위해 끙끙댈 필요는 없습니다.

따라서, 입력 데이터가 클 때는 O(n) 혹은 O(log n)의 시간 복잡도를 만족할 수 있도록 예측해서 문제를 풀어야 합니다. 그리고 주어진 데이터가 작을 때는 시간 복잡도가 크더라도 문제를 풀어내는 것에 집중.

대략적인 데이터 크기에 따른 시간 복잡도는 다음과 같습니다.

데이터 크기 제한	예상되는시간 복잡도
n ≤ 1,000,000	O(n) or O (logn)
n ≤ 10,000	O(n2)
n ≤ 500	O(n3)

2. Greedy Algorithm

Greedy는 "탐욕스러운, 욕심 많은" 이란 뜻입니다. Greedy Algorithm(탐욕 알고리즘)은 말 그대로 선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에 도달하는 방법입니다. 아래와 같이 단계적으로 구분할 수 있습니다.

선택 절차(Selection Procedure): 현재 상태에서의 최적의 해답을 선택합니다.
적절성 검사(Feasibility Check): 선택된 해가 문제의 조건을 만족하는지 검사합니다.
해답 검사(Solution Check): 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복합니다.

문제 1

김코딩은 오늘도 편의점에서 열심히 아르바이트하고 있습니다. 손님으로 온 박해커는 과자와 음료를 하나씩 집어 들었고, 물건 가격은 총 4,040원이 나왔습니다. 박해커는 계산을 하기 위해 5,000원을 내밀며, 거스름돈은 동전의 개수를 최소한으로 하여 거슬러 달라고 하였습니다.

해답 1

선택 절차 : 거스름돈의 동전 개수를 줄이기 위해 현재 가장 가치가 높은 동전을 우선 선택합니다.
적절성 검사 : 1번 과정을 통해 선택된 동전들의 합이 거슬러 줄 금액을 초과하는지 검사합니다. 초과하면 가장 마지막에 선택한 동전을 삭제하고, 1번으로 돌아가 한 단계 작은 동전을 선택합니다.
해답 검사 : 선택된 동전들의 합이 거슬러 줄 금액과 일치하는지 검사합니다. 액수가 부족하면 1번 과정부터 다시 반복합니다.

이 과정을 통해 얻은 문제에 대한 해답은 다음과 같습니다.

가장 가치가 높은 동전인 500원 1개를 먼저 거슬러 주고 잔액을 확인한 뒤, 이후 100원 4개, 50원 1개, 10원 1개의 순서대로 거슬러 줍니다.

문제 2

시장 최나무는 아파트 단지 내의 모든 동을 연결하는 새로운 도로의 건설을 계획하고 있습니다. 이때, 할당된 예산의 한계로 인해 도로는 최소의 비용으로 건설해야 합니다. 최나무는 어떻게 도로 설계를 해야 할까요? 각 동과 동을 연결하는 도로 건설 비용은 다음과 같습니다. (단, 세 개 이상의 동을 순환(cycle)하는 도로는 건설하지 않습니다.)

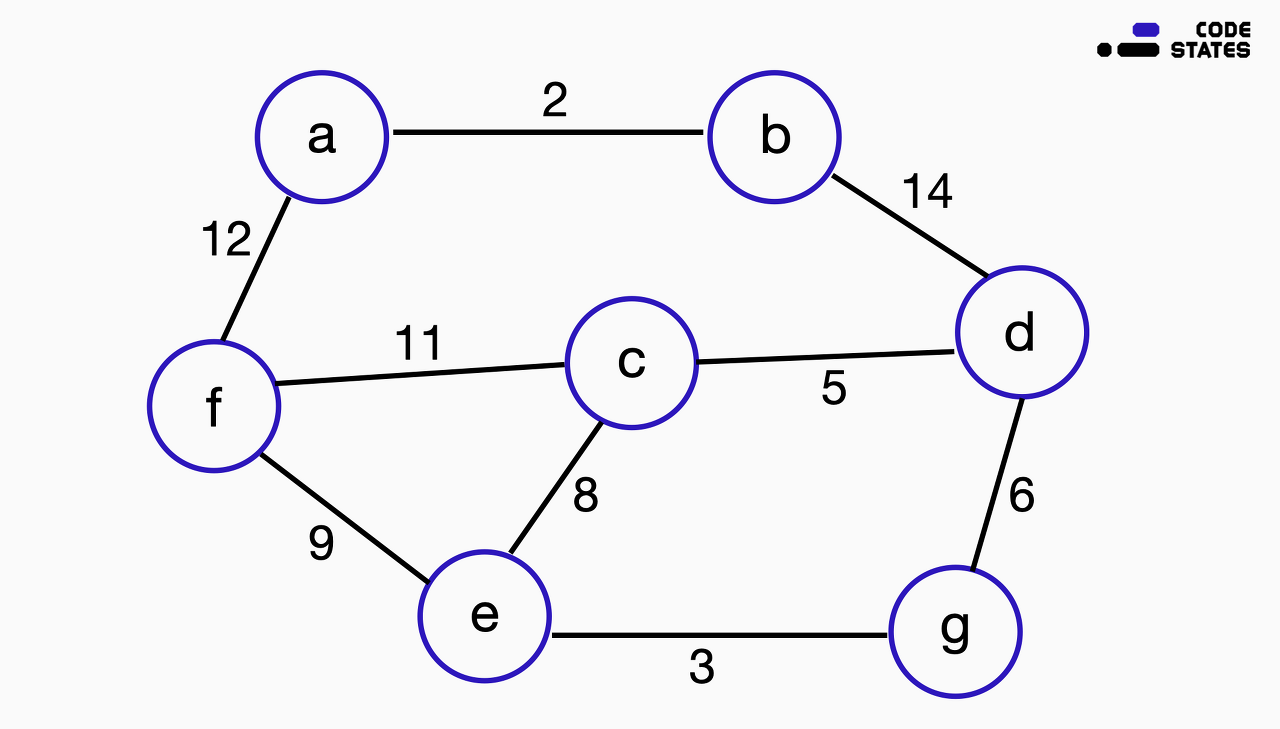
해답 2

선택 절차 : 건설 비용이 저렴한 도로를 선택합니다. 최소 비용을 구해야 하니 선택 전에 비용 순으로 오름차순 목록을 만들고 시작합니다.
적절성 검사 : 순환 여부를 검사합니다. 순환한다면 가장 마지막에 선택된 도로를 삭제하고, 1번으로 돌아가 이전 선택보다 한 단계 비싼 도로를 선택합니다.
해답 검사 : 선택된 도로들이 모든 동을 연결하는지 검사합니다. 연결되지 않은 동이 있다면 1번 과정부터 다시 반복합니다.

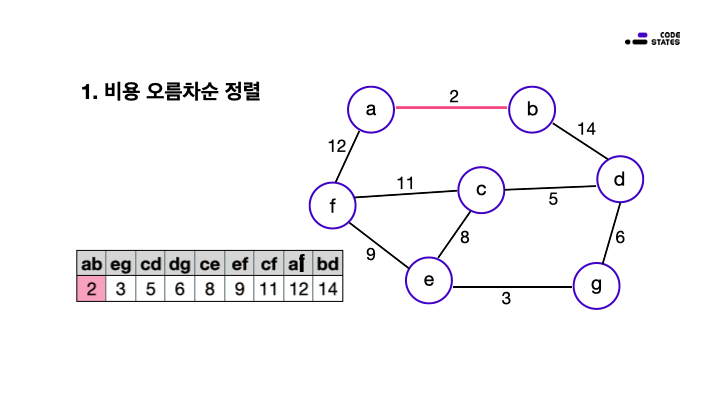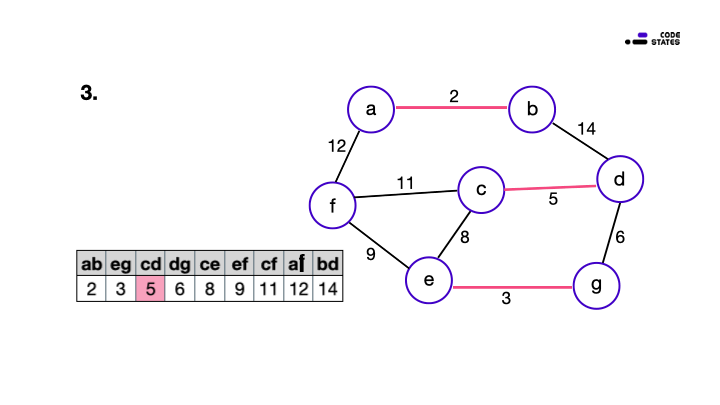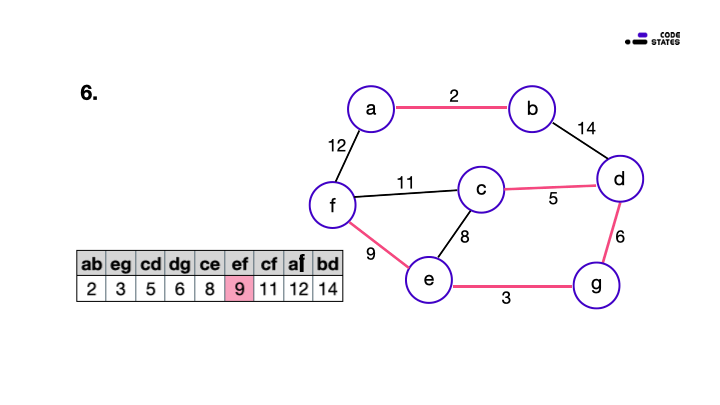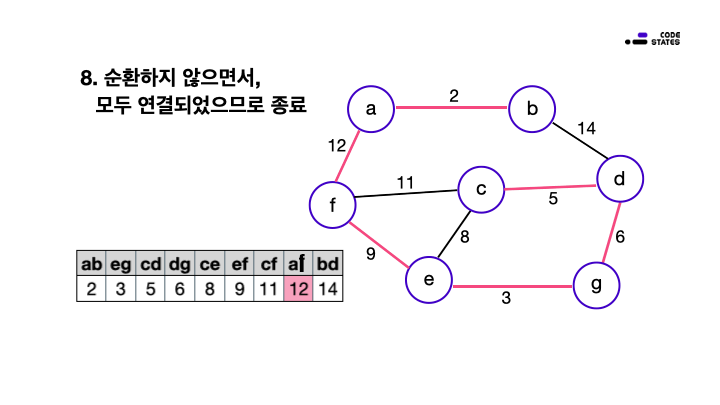
최초에 건설 비용을 오름차순으로 정리하는 과정을 추가하였지만, 현재 상태의 최적의 선택(최소 비용), 적절성 검사(순환 여부), 해답 검사(모두 연결)를 순서대로 진행하는 탐욕 알고리즘의 풀이 과정으로 이 문제를 해결할 수 있습니다. 이 문제는 도로를 건설하는데 드는 최소 비용을 구하는 문제이지만, 사실은 최소비용 신장 트리(Minimum Spanning Trees)를 만드는 문제이고, 이 풀이는 Kruskal 알고리즘을 이용한 것입니다.

탐욕 알고리즘은 기준에 따라 좋은 것을 선택하는 알고리즘이므로 그래프나 정렬, 다익스트라(Dijkstra) 알고리즘까지 폭넓은 영역에서 사용됩니다.

최소비용 신장 트리 : 그래프 내의 모든 정점을 최소 비용으로 연결하는 트리
Kruskal 알고리즘 : 최소비용 신장 트리를 만드는 알고리즘 중 탐욕 알고리즘을 이용한 풀이

문제 3

김코딩이 아르바이트를 하러 간 사이에, 안타깝게도 김코딩의 집에 도둑이 들었습니다. 도둑의 가방은 35kg까지의 물건만 담을 수 있고, 김코딩의 집에는 4개의 물건이 있습니다.

해답 3

도둑이 탐욕 알고리즘을 사용한다면 문제는 다음과 같이 간단해집니다.

1. 가방에 넣을 수 있는 물건 중 가장 비싼 물건을 넣습니다.

2. 그다음으로 넣을 수 있는 물건 중 가장 비싼 물건을 넣습니다. 이 과정을 반복합니다.

도둑의 가방은 35kg까지 담을 수 있고, 그림이 가장 비싸니 그림을 먼저 가방에 담을 수 있습니다. 남는 공간이 5kg밖에 남지 않아 더 훔칠 수 있는 물건이 없습니다. 그리고 이때 훔친 물건의 총 가치는 그림 하나의 가치와 같은 $3,000입니다. 만약 그림 대신 컴퓨터와 반지를 가방에 담았다면 어떨까요? 35kg이 넘지 않으면서 총 가치는 $3,500으로 그림 하나만 훔칠 때보다 더 많은 가치의 물건을 훔칠 수 있습니다.

탐욕 알고리즘은 문제를 해결하는 과정에서 매 순간, 최적이라 생각되는 해답(locally optimal solution)을 찾으며, 이를 토대로 최종 문제의 해답(globally optimal solution)에 도달하는 문제 해결 방식입니다.

그러나 문제 3(도둑의 예)와 같이 항상 최적의 결과를 보장하지는 못하는점을 기억해야 합니다.

따라서 두 가지의 조건을 만족하는 "특정한 상황" 이 아니면 탐욕 알고리즘은 최적의 해를 보장하지 못합니다. 탐욕 알고리즘을 적용하려면 해결하려는 문제가 다음의 2가지 조건을 성립하여야 합니다.

탐욕적 선택 속성(Greedy Choice Property) : 앞의 선택이 이후의 선택에 영향을 주지 않습니다.
최적 부분 구조(Optimal Substructure) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성됩니다.

탐욕 알고리즘은 항상 최적의 결과를 도출하는 것은 아니지만, 어느 정도 최적에 근사한 값을 빠르게 도출할 수 있는 장점이 있습니다. 이 장점으로 인해 탐욕 알고리즘은 근사 알고리즘으로 사용할 수 있습니다.

(Advanced) Dynamic Programming

크루분께서 DFS, BFS등 기본적인 것들을 마스터 하였을때에 다이나믹을 보는것이 좋다고 하셨습니다(결국 다이나믹은 어렵다!)

탐욕 알고리즘과 함께 언급하는 알고리즘으로, Dynamic Programming(DP; 동적 계획법)이 있습니다. 줄임말로는 DP라고 하는 이 알고리즘은, 탐욕 알고리즘과 같이 작은 문제에서부터 출발한다는 점은 같습니다. 그러나 탐욕 알고리즘이 매 순간 최적의 선택을 찾는 방식이라면, Dynamic Programming은 모든 경우의 수를 조합해 최적의 해법을 찾는 방식입니다.

Dynamic Programming의 원리는 간단합니다. 주어진 문제를 여러 개의 하위 문제로 나누어 풀고, 하위 문제들의 해결 방법을 결합하여 최종 문제를 해결하는 문제 해결 방식입니다. 하위 문제를 계산한 뒤 그 해결책을 저장하고, 나중에 동일한 하위 문제를 만날 경우 저장된 해결책을 적용해 계산 횟수를 줄입니다.

즉, 하나의 문제는 단 한 번만 풀도록 하는 알고리즘이 바로 이 다이내믹 프로그래밍입니다.

다이내믹 프로그래밍은 다음 두 가지 가정이 만족하는 조건에서 사용할 수 있습니다.

큰 문제를 작은 문제로 나눌 수 있고, 이 작은 문제가 중복해서 발견된다. (Overlapping Sub-problems)
작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 같다. 즉, 작은 문제에서 구한 정답을 큰 문제에서도 사용할 수 있다. (Optimal Substructure)

피보나치 수열 예시문

첫 번째 조건인 큰 문제를 작은 문제로 나눌 수 있고, 이 작은 문제가 중복해서 발견된다 (Overlapping Sub-problems) 는 큰 문제로부터 나누어진 작은 문제는 큰 문제를 해결할 때 여러 번 반복해서 사용될 수 있어야 한다 는 말과 같습니다. 이를 확인하기 위해, 피보나치 수열을 예로 살펴보겠습니다. 피보나치 수열은 첫째와 둘째 항이 1이며, 그 뒤의 모든 항은 바로 앞 두 항의 합과 같은 수열입니다. 피보나치 수열을 재귀 함수로 구현해 보면, 다음과 같이 작성할 수 있습니다.

function fib(n) {
	if(n <= 2) return 1;
	return fib(n - 1) + fib(n - 2);
}
// 1, 1, 2, 3, 5, 8...

이 함수의 계산 과정을 그림으로 살펴보면, 다음과 같습니다.

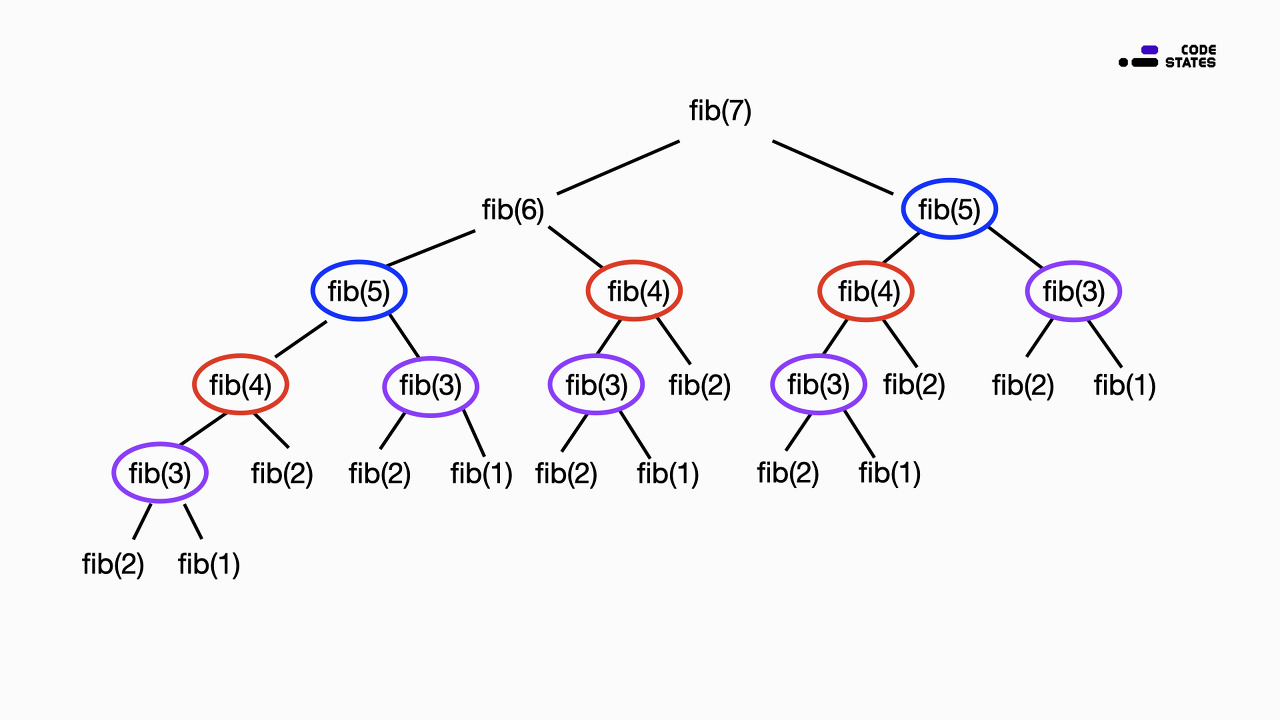
7번째 피보나치 수 fib(7) 를 구하는 과정은 다음과 같습니다.

fib(7) = fib(6) + fib(5)
fib(7) = (fib(5) + fib(4)) + fib(5) // fib(6) = fib(5) + fib(4)
fib(7) = ((fib(4) + fib(3)) + fib(4)) + (fib(4) + fib(3)) // fib(5) = fib(4) + fib(3)
.....

피보나치 수열은 위 예시처럼 동일한 계산을 반복적으로 수행해야 합니다. 이 과정에서 fib(5) 는 두 번, fib(4) 는 세 번, fib(3) 은 다섯 번의 동일한 계산을 반복합니다. 이렇게 작은 문제의 결과를 큰 문제를 해결하기 위해 여러 번 반복하여 사용할 수 있을 때, 부분 문제의 반복(Overlapping Sub-problems)이라는 조건을 만족합니다. 그러나 이 조건을 만족하는지 확인하기 전에, 한 가지 주의해야 할 점이 있습니다. 주어진 문제를 단순히 반복 계산하여 해결하는 것이 아니라, 작은 문제의 결과가 큰 문제를 해결하는 데에 여러 번 사용될 수 있어야 합니다.

두 번째 조건인 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다. 즉, 작은 문제에서 구한 정답을 큰 문제에서도 사용할 수 있다(Optimal Substructure). 에 대해 살펴보겠습니다. 이 조건에서 말하는 정답은 최적의 해결 방법(Optimal solution)을 의미합니다. 따라서 두 번째 조건을 달리 표현하면, 주어진 문제에 대한 최적의 해법을 구할 때, 주어진 문제의 작은 문제들의 최적의 해법(Optimal solution of Sub-problems)을 찾아야 합니다. 그리고 작은 문제들의 최적의 해법을 결합하면, 결국 전체 문제의 최적의 해법(Optimal solution)을 구할 수 있습니다. 최단 경로를 찾는 문제를 통해 이 조건을 살펴보겠습니다.

A에서 D로 가는 최단 경로를 찾아야 합니다. 다음과 같이 각 지점이 있고, 한 지점에서 다른 지점으로 갈 수 있는 경로와 해당 경로의 거리는 다음과 같습니다.

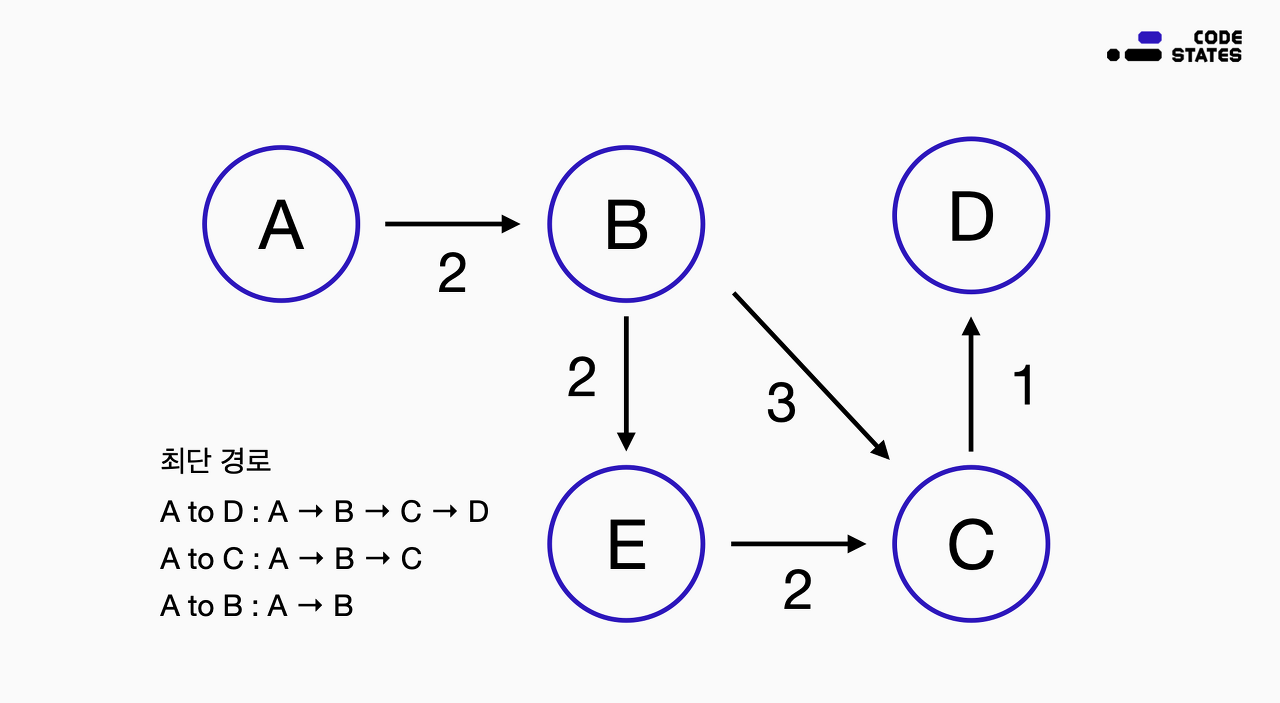
A에서 D로 가는 최단 경로는 A → B → C → D 입니다. 그렇다면 A에서 C로 가는 최단 경로는 어떨까요? A → B → E → C가 아닌 A → B → C 입니다. 마지막으로 A에서 B로 가는 최단 경로는? 당연히 A → B 입니다. 정리해보면 A에서 D로 가는 최단 경로는 그것의 작은 문제인 A에서 C로 가는 최단 경로, 그리고 한번 더 작은 문제인 A에서 B로 가는 최단 경로의 파악할 수 있습니다. 이렇게 다이내믹 프로그래밍을 적용하기 위해서는, 작은 문제의 최적 해법을 결합하여 최종 문제의 최적 해법을 구할 수 있어야 합니다.

이어지는 콘텐츠에서는 다이내믹 프로그래밍을 이용하여 피보나치 수열 문제를 해결합니다.

Recursion + Memoization

다이내믹 프로그래밍은 하위 문제의 해결책을 저장한 뒤, 동일한 하위 문제가 나왔을 경우 저장해 놓은 해결책을 이용합니다. 이때 결과를 저장하는 방법을 Memoization이라고 합니다.

Memoization의 정의는 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술 입니다.

재귀 함수에 Memorization을 적용 예시입니다.

function fibMemo(n, memo = []) {
		// 이미 해결한 하위 문제인지 찾아본다
    if(memo[n] !== undefined) return memo[n];
    if(n <= 2) return 1;
		// 없다면 재귀로 결괏값을 도출하여 res 에 할당
    let res = fibMemo(n-1, memo) + fibMemo(n-2, memo);
		// 추후 동일한 문제를 만났을 때 사용하기 위해 리턴 전에 memo 에 저장
    memo[n] = res;
    return res;
}

먼저 fibMemo 함수의 파라미터로 n 과 빈 배열을 전달합니다. 이 빈 배열은 하위 문제의 결괏값을 저장하는 데에 사용합니다.
memo 라는 빈 배열의 n번째 인덱스가 undefined 이 아니라면, 다시 말해 n 번째 인덱스에 어떤 값이 저장되어 있다면, 저장되어 있는 값을 그대로 사용합니다.
undefined라면, 즉 처음 계산하는 수라면 fibMemo(n-1, memo) + fibMemo(n-2, memo)를 이용하여 값을 계산하고, 그 결괏값을 res 라는 변수에 할당합니다.
마지막으로 res 를 리턴하기 전에 memo 의 n 번째 인덱스에 res 값을 저장합니다. 이렇게 하면 (n+1)번째의 값을 구하고 싶을 때, n번째 값을 memo 에서 확인해 사용할 수 있습니다.

위의 과정을 이미지로 표현하면 다음과 같습니다.

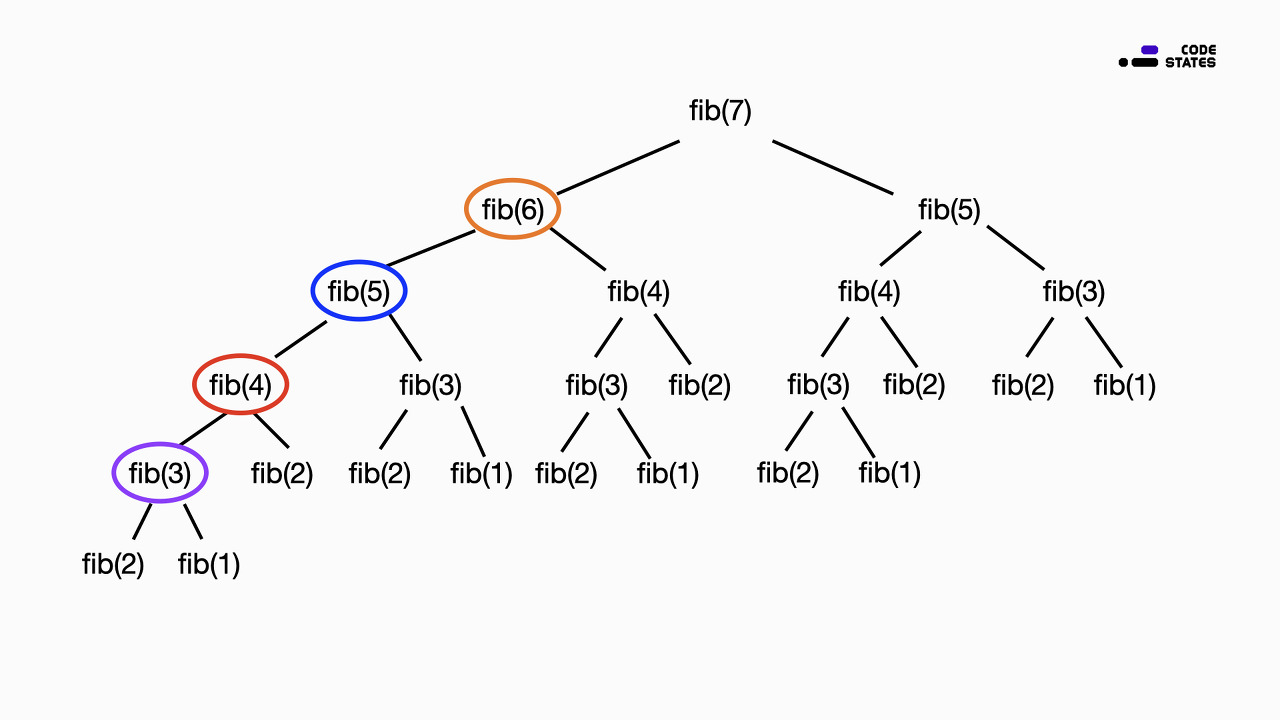
fib(7) 을 구하기 위해서는 이전의 작업으로 저장해 놓은 하위 문제의 결괏값을 사용합니다. n이 커질수록 계산해야 할 과정은 선형으로 늘어나기 때문에 시간 복잡도는 O(N) 이 됩니다. Memorization을 사용하지 않고 재귀 함수로만 문제를 풀 경우, n이 커질수록 계산해야 할 과정이 두 배씩 늘어나 시간 복잡도가 O(2^N)에 되는 것과 비교하였을 때, 다이내믹 프로그래밍의 강점을 확인할 수 있습니다.

다이내믹 프로그래밍을 적용한 피보나치 수열에서 fib(7)을 구하기 위해 fib(6)을, fib(6)을 구하기 위해 fib(5)을 호출합니다. 이런 풀이 과정이 마치, 위에서 아래로 내려가는 것과 같습니다. 큰 문제를 해결하기 위해 작은 문제를 호출한다고 하여, 이 방식을 Top-down 방식이라 부르기도 합니다.

Iteration + Tabulation

이번에는 반복문을 이용하여 다이내믹 프로그래밍을 구현합니다.

하위 문제의 결괏값을 배열에 저장하고, 필요할 때 조회하여 사용하는 것은 재귀 함수를 이용한 방법과 같습니다. 그러나 재귀 함수를 이용한 방법이 문제를 해결하기 위해 큰 문제부터 시작하여 작은 문제로 옮아가며 문제를 해결하였다면, 반복문을 이용한 방법은 작은 문제에서부터 시작하여 큰 문제를 해결해 나가는 방법입니다. 따라서 이 방식을 Bottom-up 방식이라 부르기도 합니다.

function fibTab(n) {
    if(n <= 2) return 1;
    let fibNum = [0, 1, 1];
		// n 이 1 & 2일 때의 값을 미리 배열에 저장해 놓는다
    for(let i = 3; i <= n; i++) {
        fibNum[i] = fibNum[i-1] + fibNum[i-2];
		// n >= 3 부터는 앞서 배열에 저장해 놓은 값들을 이용하여
		// n번째 피보나치 수를 구한 뒤 배열에 저장 후 리턴한다 
    }
    return fibNum[n];
}

크롬 개발자 도구에서 함수 실행 시간 측정 방법

피보나치 수열을 3가지 방법으로 구현했습니다. 이렇게 구현한 3가지 방법이 시간 복잡도를 얼마나 효과적으로 개선하였는지,

Top-down과 Bottom-up이 과연 동일한 소요 시간을 갖는지 확인하고 코드를 실행하며 결과에 대한 원인을 분석 해야합니다.

함수의 실행 시간을 측정하는 방법은 여러 가지가 있습니다. 그중에서 다음의 방법으로 간단하게 함수의 실행 시간을 확인할 수 있습니다. 실행 환경에 따라 결과가 다르므로 측정 결과는 학습 용도로만 사용하세요.

var t0 = performance.now();
fib(50); // 여기에서 함수 실행을 시켜주세요
var t1 = performance.now();
console.log("runtime: " + (t1 - t0) + 'ms')

3. Implementation

N 개의 숫자들을 특정한 기준에 맞게 순서를 조정하는 것을 정렬이라고 부르고,

그래프 탐색의 경우 탐색 방식에 따라 DFS와 BFS라고 부릅니다.

수많은 문제 해결 과정은 대부분 여러 개의 카테고리로 묶여집니다. 각 카테고리는 원하는 의도가 분명하게 있고, 그것을 해결하는 것이 목표입니다.

데이터를 정렬할 수 있는가?
데이터를 효율적으로 탐색할 수 있는가?
데이터를 조합할 수 있는가? ...etc

카테고리를 분류한다고 해도 내가 생각한 로직을 '코드로 구현'한다는 건 전부 공통적인 속성입니다. 이러한 문제 해결을 코드로 풀어낼 때, 정확하고 빠를 수록 구현 능력이 좋다고 말합니다. 구현 능력이 좋은 개발자를 선발할 의도로 구현 능력을 직접 평가하기도 합니다. '정해진 시간 안에 빠르게 문제를 해결하는 능력'을 보기 위함입니다. 머리로 이해하고 있어도 코드로 작성하지 않는다(혹은 시간 부족으로 못한다)면 정답이 될 수 없기 때문입니다.

선택한 프로그래밍 언어의 문법을 정확히 알고 있어야 하며, 문제의 조건에 전부 부합하는 코드를 실수 없이 빠르게 작성하는 것을 목표로 두는 것을 구현 문제, 구현 유형이라고 통칭할 수 있습니다.

보통 이러한 문제들은 구현하는 것 자체를 굉장히 까다롭게 만듭니다. 지문을 매우 길게 작성하거나, 까다로운 조건이나 상황을 붙인다거나, 로직은 쉽지만 구현하려는 코드가 굉장히 길어지게 되는 문제들이 대다수입니다. 그렇기 때문에 깊은 집중력과 끈기가 필요합니다.

구현 능력을 보는 대표적인 사례에는 완전 탐색(brute force)과 시뮬레이션(simulation)이 있습니다. 완전 탐색이란 가능한 모든 경우의 수를 전부 확인하여 문제를 푸는 방식을 뜻하고, 시뮬레이션은 문제에서 요구하는 복잡한 구현 요구 사항을 하나도 빠트리지 않고 코드로 옮겨, 마치 시뮬레이션을 하는 것과 동일한 모습을 그립니다.

1) 완전 탐색

모든 문제는 완전 탐색으로 풀 수 있습니다. 이 방법은 굉장히 단순하고 무식하지만 "답이 무조건 있다"는 강력함이 있습니다.

예를 들어, 양의 정수 1부터 100까지의 임의의 요소가 오름차순으로 하나씩 담긴 배열 중, 원하는 값 N을 찾기 위해서는 배열의 첫 요소부터 마지막 요소까지 전부 확인을 한다면 최대 100 번의 탐색 끝에 원하는 값을 찾을 수 있습니다.

문제 해결을 할 때엔 기본적으로 두 가지 규칙을 적용합니다.

1. 문제를 해결할 수 있는가? 2. 효율적으로 동작하는가?

완전 탐색은 첫 번째 규칙을 만족시킬 수 있는 강력한 무기이지만 두 번째 규칙은 만족할 수 없는 경우가 있습니다.

문제

양의 정수 1부터 100까지의 임의의 요소가 오름차순으로 하나씩 담긴 배열 중, 원하는 값 N을 찾으시오. 단, 시간 복잡도가 O(N)보다 낮아야 합니다.

위의 문제에 최악의 경우 100 번을 시도해야 하는 완전 탐색은 두 번째 규칙을 만족할 수 없습니다.

배열을 작은 수에서 큰 수, 혹은 그 반대로 정렬한 후 이분 탐색을 사용하는 방법 등 다른 알고리즘을 사용해야 합니다. 문제를 풀 수 있는 가능한 모든 방법을 고려한 후 효율적으로 동작하는 알고리즘이 전부 탐색할 수밖에 없다고 판단될 때 적용할 수 있습니다.

완전 탐색은 단순히 모든 경우의 수를 탐색하는 모든 경우를 통칭합니다.

완전히 탐색하는 방법에는 brute Force(조건/반복을 사용하여 해결), 재귀, 순열, DFS/BFS 등 여러 가지가 있습니다. 우리는 그중, Brute Froce(무차별 대입)에 대해 예시를 들어보겠습니다.

문제

우리 집에는 세 명의 아이들이 있습니다. 아이들의 식성은 까다로워, 먹기 싫은 음식과 좋아하는 음식을 철저하게 구분합니다. 먹기 싫은 음식이 식탁에 올라왔을 땐 음식 냄새가 난다며 그 주변의 음식까지 전부 먹지 않고, 좋아하는 음식이 올라왔을 땐 해당 음식을 먹어야 합니다. 세 아이의 식성은 이렇습니다.

첫째: (싫어하는 음식 - 미역국, 카레) (좋아하는 음식 - 소고기, 된장국, 사과)

둘째: (싫어하는 음식 - 참치, 카레) (좋아하는 음식 - 미역국, 된장국, 바나나)

셋째: (싫어하는 음식 - 소고기) (좋아하는 음식 - 돼지고기, 된장국, 참치)

100 개의 반찬이 일렬로 랜덤하게 담긴 상이 차려지고, 한 명씩 전부 먹을 수 있다고 할 때, 가장 많이 먹게 되는 아이와 가장 적게 먹게 되는 아이는 누구일까요? (단, 그 주변의 음식은 반찬의 앞, 뒤로 한정합니다.)

해설

이 문제는 단순히 100 개의 반찬을 첫째, 둘째, 셋째의 식성에 맞게 하나씩 대입하여 풀 수 있습니다.

각각 몇 가지 음식을 얼마나 먹을 수 있는지 각각 계산한 후, 제일 많이 먹는 아이와 제일 적게 먹는 아이를 파악할 수 있습니다. 문제를 풀 때, 반복문이 아닌 배열을 전부 순회하는 메서드를 사용한다거나 간결한 코드를 위한 문법을 사용한다고 하더라도 배열을 전부 탐색하여 세 명의 값을 도출한다는 것엔 변함이 없습니다.

코드

for(let i = 0; i < 100; i++) {
  if(첫째 식성) {
    if(싫어하는 음식이 앞뒤로 있는가) {
      그냥 넘어가자;
    }
    좋아하는 음식 카운트;
  }
  if(둘째 식성) {
    if(싫어하는 음식이 앞뒤로 있는가) {
      그냥 넘어가자;
    }
    좋아하는 음식 카운트;
  }
  if(셋째 식성) {
    if(싫어하는 음식이 앞뒤로 있는가) {
      그냥 넘어가자;
    }
    좋아하는 음식 카운트;
  }
}

return 많이 먹은 아이;

2) 시뮬레이션

시뮬레이션은 모든 과정과 조건이 제시되어, 그 과정을 거친 결과가 무엇인지 확인하는 유형입니다. 보통 문제에서 설명해 준 로직 그대로 코드로 작성하면 되어서 문제 해결을 떠올리는 것 자체는 쉬울 수 있으나 길고 자세하여 코드로 옮기는 작업이 까다로울 수 있습니다.

문제에 대한 이해를 바탕으로 제시하는 조건을 하나도 빠짐없이 처리해야 정답을 받을 수 있습니다. 하나라도 놓친다면 통과할 수 없게 되고, 길어진 코드 때문에 헷갈릴 수도 있으니 주의해야 합니다.

문제

무엇을 위한 조직인지는 모르겠지만, 비밀스러운 비밀 조직 '시크릿 에이전시'는 소통의 흔적을 남기지 않기 위해 3 일에 한 번씩 사라지는 메신저 앱을 사용했습니다. 그러나 내부 스파이의 대화 유출로 인해 대화를 할 때 조건을 여러 개 붙이기로 했습니다. 해당 조건은 이렇습니다.

캐릭터는 아이디, 닉네임, 소속이 영문으로 담긴 배열로 구분합니다.
소속은 'true', 'false', 'null' 중 하나입니다.
소속이 셋 중 하나가 아니라면 아이디, 닉네임, 소속, 대화 내용의 문자열을 전부 X로 바꿉니다.
아이디와 닉네임은, 길이를 2진수로 바꾼 뒤, 바뀐 숫자를 더합니다.
캐릭터와 대화 내용을 구분할 땐 공백:공백으로 구분합니다: ['Blue', 'Green', 'null'] : hello.
띄어쓰기 포함, 대화 내용이 10 글자가 넘을 때, 내용에 .,-+ 이 있다면 삭제합니다.
띄어쓰기 포함, 대화 내용이 10 글자가 넘지 않을 때, 내용에 .,-+@#$%^&*?! 이 있다면 삭제합니다.
띄어쓰기를 기준으로 문자열을 반전합니다: 'abc' -> 'cba'
띄어쓰기를 기준으로 소문자와 대문자를 반전합니다: 'Abc' -> 'aBC'

시크릿 에이전시의 바뀌기 전 대화를 받아, 해당 조건들을 전부 수렴하여 수정한 대화를 객체에 키와 값으로 담아 반환하세요. 같은 캐릭터가 두 번 말했다면, 공백을 한 칸 둔 채로 대화 내용에 추가되어야 합니다. 대화는 문자열로 제공되며, 하이픈- 으로 구분됩니다.

문자열은 전부 싱글 쿼터로 제공되며, 전체를 감싸는 문자열은 더블 쿼터로 제공됩니다.

예: "['Blue', 'Green', 'null'] : 'hello. im G.' - ['Black', 'red', 'true']: '? what? who are you?'"

대화 내용이 담긴 문자열을 입력받아, 문자열을 파싱하여 재구성을 하려고 합니다.

해설

예시를 이용하여 순차적으로 작성해 봅시다.

"['Blue', 'Green', 'null'] : 'hello. im G.' - ['Black', 'red', 'true']: '? what? who are you?'" 입력값으로 받은 문자열을 각 캐릭터와 대화에 맞게 문자열로 파싱을 하고, 파싱한 문자열을 상대로 캐릭터와 대화를 구분합니다.
- 첫 번째 파싱은 - 을 기준으로 ['Blue', 'Green', 'null'] : 'hello. im G.', ['Black', 'red', 'true']: '? what? who are you?' 두 부분으로 나눕니다.
- 두 번째 파싱은 : 을 기준으로 ['Blue', 'Green', 'null'] 배열과 'hello. im G.' 문자열로 나눕니다.
배열과 문자열을 사용해, 조건에 맞게 변형합니다.
- 소속이 셋 중 하나인가 판별합니다.
- ['Blue', 'Green', 'null'] 아이디와 닉네임의 길이를 2진수로 바꾼 뒤, 숫자를 더합니다: [1, 2, 'null']
- 'hello. im G.' 10 글자가 넘기 때문에, .,-+@#$%^&* 를 삭제합니다: 'hello im G'
- 'hello im G' 띄어쓰기를 기준으로 문자열을 반전합니다: 'olleh mi G'
- 'olleh mi G' 소문자와 대문자를 반전합니다: 'OLLEH MI g'
변형한 배열과 문자열을 키와 값으로 받아 객체에 넣습니다.
- { "[1, 2, 'null']": 'OLLEH MI g' }

다음 내용

Algorithm with Math, 정규표현식

'코테 > 자료구조, 알고리즘' 카테고리의 다른 글

[알고리즘] 소수 판별식 (에라토스테네스의 체) (0)	2021.07.21
[알고리즘] Algorithm with Math / 정규표현식 (0)	2021.07.21
[알고리즘] Graph / Tree / BST (1)	2021.06.19
[자료구조] 자료구조 기초 Stack, Queue (2)	2021.06.17
[자료구조/알고리즘] JSON, Tree UI, 재귀함수 과제 (0)	2021.06.16